Les trix
Publié : mar. 7/01/2025 13:29
Les trix
Un trix est un nombre qui s'écrit avec le chiffre '4' et les 8 opérations suivantes E = { +, -, x, /, √, ab, !, [x] }
Rappel
√4 = 2
23 = 2x2x2 = 8
5! = 5x4x3x2x1 = 120
[7,1485] = 7 ; [x]=partie entière de x (l'entier immédiatement avant x)
par ex:
\[ \frac{4!(4+\sqrt{4})}{4+4!} - 4^{\sqrt{4}} \]
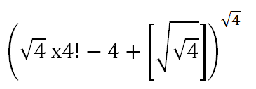
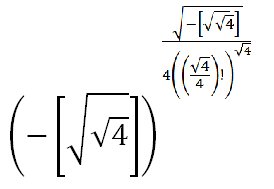
NOTE:
-Les parenthèses '(', ')' sont autorisées , c'est juste pour la visibilité des lectures.
-Les écritures 44, 444, 4444, ... ne sont pas autorisées
La fabrication des trix ressemble beaucoup à la construction des nombres
constructibles, des radicaux, des propositions (en logique) ...
En effet au départ on a un petit ensemble A, et les opérations E, puis on construit des ensembles de plus en plus grands à partir de ces opérations avec des nombres déjà construits
Par exemple pour les nombres constructibles on a:
A = {1} ensemble de départ
E = { +, -, x, /, √ } opérations
Et l'ensemble qu'on obtient c'est les nombres constructibles (à la règle et au compas) !!!
par ex:
(1+√5)/2
Pour les radicaux on a:
A = {1} ensemble de départ
E = { +, -, x, /, n√ = racine n-ième } opérations
Et l'ensemble qu'on obtient c'est les radicaux, les solutions des équations-polynomiales résolubles !!!
par ex:
\[ \sqrt[3]{1-\sqrt{5}} + \sqrt[3]{1+\sqrt{5}} \]
Pour les propositions on a:
A = {p,q,r,...} ensemble de départ (infini)
E = { ⌉ , Λ , V , → , ↔ } opérations
Et l'ensemble qu'on obtient c'est l'ensemble des propositions (en logique).
par ex :
(p → q) → ⌉r
Un trix est un nombre qui s'écrit avec le chiffre '4' et les 8 opérations suivantes E = { +, -, x, /, √, ab, !, [x] }
Rappel
√4 = 2
23 = 2x2x2 = 8
5! = 5x4x3x2x1 = 120
[7,1485] = 7 ; [x]=partie entière de x (l'entier immédiatement avant x)
par ex:
\[ \frac{4!(4+\sqrt{4})}{4+4!} - 4^{\sqrt{4}} \]
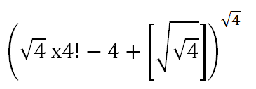
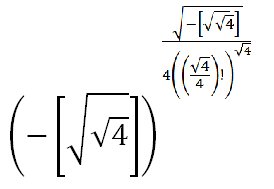
NOTE:
-Les parenthèses '(', ')' sont autorisées , c'est juste pour la visibilité des lectures.
-Les écritures 44, 444, 4444, ... ne sont pas autorisées
La fabrication des trix ressemble beaucoup à la construction des nombres
constructibles, des radicaux, des propositions (en logique) ...
En effet au départ on a un petit ensemble A, et les opérations E, puis on construit des ensembles de plus en plus grands à partir de ces opérations avec des nombres déjà construits
Par exemple pour les nombres constructibles on a:
A = {1} ensemble de départ
E = { +, -, x, /, √ } opérations
Et l'ensemble qu'on obtient c'est les nombres constructibles (à la règle et au compas) !!!
par ex:
(1+√5)/2
Pour les radicaux on a:
A = {1} ensemble de départ
E = { +, -, x, /, n√ = racine n-ième } opérations
Et l'ensemble qu'on obtient c'est les radicaux, les solutions des équations-polynomiales résolubles !!!
par ex:
\[ \sqrt[3]{1-\sqrt{5}} + \sqrt[3]{1+\sqrt{5}} \]
Pour les propositions on a:
A = {p,q,r,...} ensemble de départ (infini)
E = { ⌉ , Λ , V , → , ↔ } opérations
Et l'ensemble qu'on obtient c'est l'ensemble des propositions (en logique).
par ex :
(p → q) → ⌉r