01 Dec 2025


Bienvenue sur NombreJador ...

Il est vraiment extraordinaire que l'homme puisse concevoir la notion de "nombre" et de trouver de plus en plus des nombres de toute sorte et leurs propriétés...
L'histoire des nombres est immense comme l'histoire de l'humanité, beaucoups de gens passent leur temps à chercher, à chercher...
Alors on se demande toutjours: existe-t-il encore d'autres nombres ????

18 Jan 2025

Les nombres à voir ....
e, i, π, √2, Φ, γ, ω, η, ... Chaqu'un a une définition plus ou moins étrange, mais ce qui est extaordinaire c'est qu'il existe toujours une formule reliant ces deux êtres (donc entre eux). Tout nombre est donc en relation ... Le plus célèbre est sûrement π le suivant est peut-être √2, puis e, i, Φ, ... et γ, ω, η... ω est la demi longueur da la lemniscate, une courbe d'une forme d'un 8 couché (infini = ∞) il joue le même rôle que π la demi longueur du cercle. Tandis que η est la limite d'une certaine suite découverte par Gauss à la suite sur la question: "peut on diviser la lemniscate en partie égales comme le cercle ?"

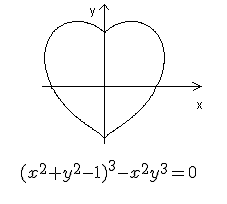L' équation d'un coeur ! Il est quand même étonnant que le coeur aie une équation !!!
\((x^2+y^2-1)^3-x^2y^3 = 0 \)

MathJax MathJax permet d'écire les formules mathématiques sur un site web, il utilise un langage spécial (le LaTeX) pour transformer l'écriture en image. Le plus simple c'est utiliser le serveur publique de MathJax.org :
Alors la syntaxe est très simple:
on place

<head>
<script id="MathJax-script" async src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js"></script>
...
</head>

¤ La formule entre \\( ... \\) donne sur la même ligne :
par ex :
Voici la formule \\( \Gamma(x)=\int_0^\infty t^{x-1} e^{-t} dt \\) , x>0, à connaitre

ça donne :
Voici la formule \( \Gamma(x)=\int_0^\infty t^{x-1} e^{-t} dt \) , x>0, à connaitre

¤ Et la formule entre \\[ ... \\] donne sur la ligne suivante et centré :
par ex :
\\[ \pi=2\int_{0}^1 \frac{dx}{\sqrt{1-x²}} \\]

\[ \pi=2\int_{0}^1 \frac{dx}{\sqrt{1-x²}} \]

En analogie avec le pi-script ω (demi-longueur de la lemniscate)
\[ \omega=2\int_{0}^1 \frac{dx}{\sqrt{1-x^4}} \]

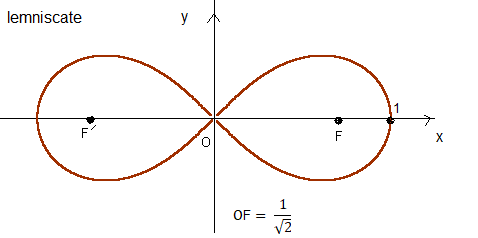L'équation cartésienne de la lemniscate :
(x²+y²)² = x² - y²

L'équation polaire de la lemniscate :
ρ² = cos 2θ

Gauss On pose :
a0 = √2 , b0 = 1
an+1 = (an + bn)/2
bn+1 = √(an bn)
On a 2 suites adjacentes elles ont donc la même limite qu'on note η
\[ \lim_{n \to +\infty} a_n = \lim_{n \to +\infty} b_n = \eta \] Gauss démontre alors cette belle formule:
\[ \frac{\pi}{\omega} = \eta \]
Et voici 2 jolies formules :
\[ n! = \int_0^\infty t^n e^{-t} dt \]
\[ (\frac{1}{2})! = \frac{\sqrt{\pi}}{2} \]

Fermat Fermat affirme que :
1) L'équation suivante n'a qu'une seule solution : x=3, y=5
y² = x3 - 2

2) L'équation suivante n'a que 2 solutions : (x=2, y=2) , (x=5, y=11)
y² = x3 - 4

saurons nous démontrer ??
Ce sont des courbes elliptiques !!









Géométrie Analytique

Arithmétique

Algèbre

Les graphes