Géométrie analytique

Difficulté: 4.7/20 facile

Géométrie analytique

Dans le plan \(\mathbb{P}\), on ne peut pas faire des calculs !! par exp on peut peut pas additionner 2 points A+B=?? , on peut seulement faire des raisonnements purs en géométrie. On aimerait bien de pouvoir faire des calculs sur les points, pour ça, on munit le plan \(\mathbb{P}\) un repère orthonormé R(O,I,J) , une fois le plan dispose un repère les points du plan sont répérés par R et les calculs deviennent alors possible.


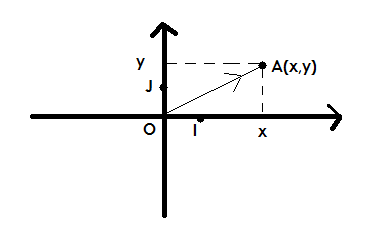
le point A(x,y) a pour coordonnées x = abscisse, et y = ordonnée ceci revient à dire que le vecteur
\( \overrightarrow{OA}=(x,y) \)
a pour composantes (x,y) . On a "vectorisé" le plan, le rendant ainsi comme un espace-vectotiel, un point A c'est comme le vecteur
\(\overrightarrow{OA} \)

Règle de calculs

1. Fabrication un vecteur
Fabrication un vecteur à partir de deux points A(x_A,y_A) et B(x_B,y_B)
\( \overrightarrow{AB}=(x_B-x_A,y_B-y_A) \)
C'est une règle très simple (on dit B-A)

2. Egalité de 2 vecteurs
\( \overrightarrow{u}(a,b)=\overrightarrow{v}(c,d) \to a=c \;et\; b=d \)
\( \overrightarrow{AB}=\overrightarrow{CD} \; \)
\( x_B-x_A=x_D-x_C \; \)
\( y_B-y_A=y_D-y_C \; \)

Le milieu de 2 points

Deux points A(x_A,y_A) , B(x_B,y_B) le milieu I(x_I,y_I) de [AB] est:
\[ x_I=\frac{x_A+x_B}{2} \;et\; y_I= \frac{y_A+y_B}{2} \]

Trois points alignés

Trois points A(x_A,y_A) , B(x_B,y_B) et C(x_C,y_C) sont alignés si on a:
\[ \frac{x_A-x_B}{y_A-y_B} = \frac{x_A-x_C}{y_A-y_C} \]
ou encore , une autre façon de dire , les vecteurs
\( \overrightarrow{AB}=(x,y) \;et\; \overrightarrow{AC}=(p,q) \)
sont colinéraires càd le dét( \(\overrightarrow{AB}\),\(\overrightarrow{AC}\) ) est nul
\( \begin{vmatrix} x & p \\ y & q \end{vmatrix} = xq-yp = 0 \)

Equation d'une droite

Une droite (D) , a une équation de la forme:
(D): ax + by + c = 0 avec a≠0 et b≠ 0
le vecteur directeur \( \vec{u}(-b,a) \) et un vecteur perpendiculaire à la droite \( \vec{n}(a,b) \)

I. On écrire l'équation de la droite à partir d'un point A(s,t) et un vecteur directeur \( \vec{u}(p,q) \)
1. On calcule le vecteur
\( \overrightarrow{AM}=(x-s,y-t)\)
2. On dit que les vecteurs \( \overrightarrow{AM} \) et \( \overrightarrow{u} \) sont colinéaires
\(\begin{vmatrix} x-s & p \\ y-t & q \end{vmatrix} = (x-s)q - (y-t)p = 0 \)

II. Equation de la droite (AB) où A(s,t), B(c,d)
1. On prend le vecteur \(\overrightarrow{AB}\) comme vecteur directeur
\( \overrightarrow{AB}=(p,q) \)
2. On calcule le vecteur
\( \overrightarrow{AM}=(x-s,y-t) \)
3. On dit que les vecteurs \(\overrightarrow{AM}\) et \(\overrightarrow{AB}\) sont colinéaires
\( \begin{vmatrix} x-s & p \\ y-t & q \end{vmatrix} = (x-s)q - (y-t)p = 0 \)

Fonction affine

Si (D) a la forme particulière
(D): y = ax + b , a=coefficient directeur et b=ordonnée
la droite provient d'une fonction affine f(x)=ax+b

la droite (D) déterminée pas deux points A(s,t) , B(c,d), pour retrouver f(x) on écrit:
f(s) = t
f(c) = d

as + b = t
ac + b = d
On trouve a,b en résolvant le système

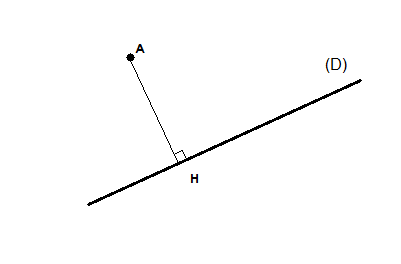
Distance d'un point à une droite

Soit (D) une droite d'équation ax + by + c = 0 et un point A(s,t)
la distance de A à (D) est données par:

\[ AH=\frac{|as+bt+c|}{\sqrt{a^2+b^2}} \]

[1] 2

Accueil

DMJ: 15/01/2025